等差坐标型
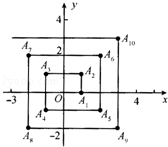
1.如图，所有正三角形的一边平行于
轴，一顶点在
轴上，从内到外，它们的边长依次为，…，顶点依次用
，…，表示，其中
与
轴、底边与
、与
、…均相距一个单位，则顶点
的坐标是___________，的坐标是______．
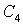
分析：
依据已知
的边长为2，且底边
与轴相距一个单位.
，又可求出
.
,且点
的坐标为
.
因为
余
，而
的坐标为 ，
的坐标为
的坐标为
……
的坐标为
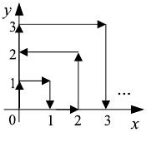
2.如图，在平面直角坐标系中，一动点从原点
出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点
，
，
，
，…那样点的坐标为_____
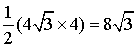
分析：由图可知，
时
，
，点
，
时，，点，
时，
，点，
所以，点
．
故答案为：．
3.如图，已知正方形 ，顶点
．规定“把正方形 先沿轴翻折，再向左平移
个单位”为一次变换．这样如此，连续经过次变换后，正方形的对角线交点的坐标变为
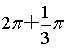
分析：∵正方形 ，点 、 、 ．
∴ 的坐标变为
∴依据题意得：
第次变换后的点的对应点的坐标为
，即，
第次变换后的点的对应点的坐标为：，即
，
第
次变换后的点的对应点的坐标为
，即，
第 次变换后的点 的对应点的为坐标为
，即
4.如图，动点
在平面直角坐标系中按图中箭头所示方向运动，第次从原点运动到
点
，第次接着运动到点
，第次接着运动到点
，……，按如此的运动规律，经过第次运动后，动点的坐标是（ ）．
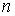
A．
B．
C．
D．
答案：A
分析：由已知找出规律：
运动的点的横坐标等于它运动的次数；
它的纵坐标依据运动次数的奇偶性确定，
奇数次时，若满足，纵坐标为1，
若满足，纵坐标为2
偶奇数次时纵坐标为
.
按如此的运动规律，经过第次运动后，
由于
，
所以动点的坐标是 .
5.如图，已知
，则点的坐标是多少．
答案：-502；-502
分析：易得4的整数倍的各点如 等点在第三象限，
∵；
∴的坐标在第三象限，
横坐标为；纵坐标为
，
∴点的坐标是
．
故答案为：．
6.一只跳蚤在第一象限及轴、轴上跳动，在第一秒钟，它从原点跳动到，然后接着按图中箭头所示方向跳动[即→→→→…，且每秒跳动一个单位，那样第秒时跳蚤所在地方的坐标是（ ）
A． B． C． D．
答案：C
分析：办法1、在演草纸上按规律去画.
办法2、依据题意，结合图形
大家可以发现第
秒时
跳蚤所在地方的坐标是：
①为奇数时，坐标为
，
②为偶数时，坐标为
，
所以需要坐标为.
7.在平面直角坐标系
中，大家把横、纵坐标都是整数的点叫做整点．已知点，点
是轴正半轴上的整点，记内部（不包含边界）的整点个数为．当时，点的坐标是多少；当点的横坐标为（为正整数）时，_____（用含的代数式表示．）
答案：3；4；6n-3,-3+6n
分析：
如图：
当点在点或
点时，内部（不包含边界）的整点为
，共三个点，
所以当时，点的横坐标的所大概值是或
；
当点的横坐标为
时，时，内部（不包含边界）的整点个数，
当点的横坐标为
时，时，内部（不包含边界）的整点个数，
所以当点的横坐标为（为正整数）时，；
另解：网格点横向一共行，竖向一共是列，所以在轴和点形成的矩形内部一共有个网格点，而这条连线为矩形的对角线，与条横线有个网格点相交，所以要减掉点，总的来讲就是矩形内部网格点减掉点的一半，即为
．
故答案为：或，．
8.如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“”方向排列，如
…依据这个规律探索可得，第20个点的坐标是___；第90个点的坐标为_____．
分析：横坐标为1的点有1个，纵坐标只不过0；横坐标为2的点有2个，纵坐标是0或1；横坐标为3的点有3个，纵坐标分别是0，1，2…横坐标为奇数，纵坐标从大数开始数；横坐标为偶数，则从0开始数．
9.在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．请你察看图中正方形每一个正方形四条边上的整点的个数．按此规律推算出正方形
四条边上的整点共有______个．
答案：80
分析：
依据图象,
正方形四条边上的整数点有8个；
正方形四条边上的整数点有16个；
正方形四条边上的整数点有24个；
以此类推可发现每次增大8个，
所以正方形正方形四条边上的整数点有
个.
当时，正方形四条边上的整数点共有80个.
10.如图，二次函数的图象，记为，它与轴交于点、；将绕点旋转得，交轴于点；将绕点旋转得，交轴于点；……这样进行下去，直至得．若在第段图象上，则______．
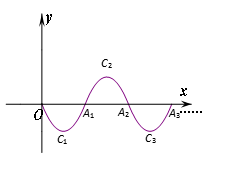
答案：
分析：依题可知，，，
……；
，，
，，，……
．
故答案为：．
11.如图， 与 轴相切于点 ，点 的坐标为 ，点 在 上，且在第一象限， ， 沿 轴正方向滚动，当点 第 次落在 轴上时，求点 的横坐标．
分析：依据扇形弧长分式，，
所以点 第 次落在 轴上时，点 的横坐标为，
点第
次落在 轴上时，点 的横坐标为，
第 次落在 轴上时，点 的横坐标为，
…，第 次落在 轴上时，
点 的横坐标为.
12.如图1，是由方向线一组同心、等距圆组成的点的地方记录图．包含8个方向：东、南、西、北、东南、东北、西南、西北，方向线交点为，以为圆心、等距的圆由内向外分别称作1、2、3、…．将点所处的圆和方向称作点的地方，比如（2，西北），（5，南），则P点地方为__________．如图2，若将（1，东）标记为点，在圆1上按逆时针方向旋转交点依次标记为；到后进入圆2，将（2，东）标记为，继续在圆2上按逆时针方向旋转交点依次标记为；到后进入圆3，之后重复以上操作过程．则点
的地方为_____，点的地方为______，点（ 为正整数）的地方为_____．
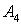
分析：
由题意得出：
点在第个圆上，且在东北方向，
故点地方为：，
由题意可得出每个数点向外移动一次，
，故点所在地方与方向相同，故点的地方为，
，故点所在地方与方向相同，故点的地方为，
，故点所在地方与方向相同，故点的地方为，
故答案为：，．
13.如图，在平面直角坐标系中，是以为圆心，2为半径的圆与过点（0，1）且平行于x轴的直线l1的一个交点；是以原点为圆心，3为半径的圆与过点（0，－2），且平行于x轴的直线l2的一个交点；是以原点为圆心，4为半径的圆与过点（0，3）且平行于x轴的直线l3的一个交点；是以原点为圆心，5为半径的圆与过点（0，－4）且平行于x轴的直线l4的一个交点；……，且点、、
、、…都在y轴右边，根据如此的规律进行下去，点的坐标为______，点的坐标为______．
分析：依据题意，可以第一求得的坐标，从中找出规律，得出的坐标
，再把代入即可求出答案．
14.如图，在平面直角坐标系中，点在第一象限，点在轴的正半轴上，．
是的内切圆，且的坐标为
．
的长为______，的长为______；点在的延长线上，交轴于点．将沿水平方向向右平移2个单位得到，将沿水平方向向右平移2个单位得到，根据同样的办法继续操作，依次得到．若 均在的内部，且恰好与相切，则此时的长为_____．（用含的式子表示）
[来源:Z+xx+k.Com]
答案：4；5；2n+3,3+2n
分析：本题需要了解三角形内切圆的圆心是三角形三个内角平分线的交点，所以内心到三角形的三条边的距离都相等．本题还考查了切线长定理的内容：从圆外一点引圆的两条切线，切线长相等．本题依据切线长相等的特征，就能求出、的长度．第二问的困难程度较小，仅需了解平移到时是由向右平移个单位得到的即可．
15.如图，在平面直角坐标系中，已知抛物线在轴上方的部分，记作，它与交于，，将绕点旋转得，与轴交于另一个点，请继续操作并探究：将绕点旋转得，与轴交于另一个点；将绕点旋转得，与轴交于另一个点．如此依次得到轴上的点，，，…，，…，即抛物线，，，…，，…，则点的坐标为_______；的顶点坐标为_______（为正整数，用含的代数式表示）．
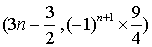
分析：依题可得，
，，，，…，；
的顶点坐标为，的顶点坐标为
，的顶点坐标为，
的顶点坐标为
，的顶点坐标为，的顶点坐标为．
故答案为：，（为正整数）．
16.如图，所有正三角形的一边平行于轴，一顶点在轴上．从内到外，它们的边长依次为，，，……，顶点依次用，，，，……表示，其中轴与边，边与，与，…均相距一个单位，则顶点的坐标为__________；的坐标为__________；的坐标为__________．
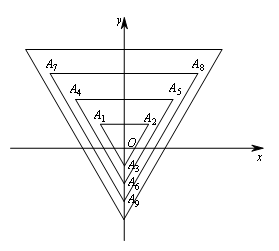
分析：，等边三角形边长为，高为，．
，，，它们在这条直线上，．
故答案为：，，．
17.大家把图（1）称作正六边形的基本图，将此基本图不断复制并平移，使得相邻两个
基本图的一边重合，如此得到图（2），图（3），…，这样进行下去，直至得图（n）．
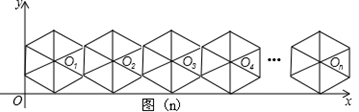
（2）将图（n）放在直角坐标系中，设其中第一个基本图的对称中心的坐标为，则__________；
（2）图（n）的对称中心的横坐标为__________．
分析：（2）如图，过点作轴于点，
∵正六边形的中心角，
，
∴，，
，
∴；
（2）由题意，可得图（2）的对称中心的横坐标为
，
图（3）的对称中心的横坐标为
，
图（4）的对称中心的横坐标为，
……
图（n）的对称中心的横坐标为．[来源:学_科_网Z_X_X_K]
故答案为：；．
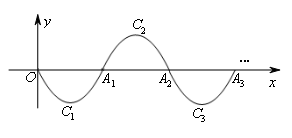
18.如图，一段抛物线：（），记为，它与轴交于点，；
将绕点旋转得，交轴于点；[来源:学*科*网Z*X*X*K]
将绕点旋转得，交轴于点；…，这样进行下去，直至得．
（）请写出抛物线的分析式：
（）若在第段抛物线上，则_____．
分析：（1）∵一般抛物线：（），记为，它与轴交于点，；
将绕点旋转得，[来源:Z。xx。k.Com]
∴过，两点，
∴抛物线的分析式二次项系数为：，且过，，
∴．
（2）∵一般抛物线：（），
∴图象与轴交点坐标为：，，
∵将绕点旋转得，交轴于点；
将绕点旋转得，交轴于点；
……[来源:学">这样进行下去，直至得．
∴的与轴的交点横坐标为，，且图象在轴上方，
∴的分析式为：，
当时，．
